|
Fortsetzung:
Ableitung der alten Längeneinheiten und deren rechnerisches Verhältnis
Anfang des Kapitels Ableitung
XII Die 30-digiti-Elle des Gudea-Maßes ideal ist 16,587 mm x 30 = 497,63 mm lang. Obwohl sie als 30-digiti-Elle konzipiert ist, hat man sie anderenorts und zu anderer Zeit in nur 28 digiti geteilt, wodurch der digitus497,63 mm : 28 = 17,773 mm lang wurde, also wuchs.
Zu noch anderer Gelegenheit rekonstruierte man aus dem nun angewachsenen digitus eine 30-digiti-Elle: 30 x 17,773 mm = 533,18 mm. Das ist die Große Ptolemäische Elle mit dem Code E1.
Diese Elle war weit verbreitet und wurde lange Zeit verwendet, weswegen sie sich viele Umformungen gefallen lassen musste. In 28 digiti aufgeteilt, wird dieser 533,18 : 28 = 19,041 mm lang. Der 16-digiti-Fuß dazu ist deshalb 304,67 mm lang. Hierin ist unschwer der heutige Englische Fuß zu erkennen, der allerdings nach Landessitte in 12 Unzen (inches zu 25,389 mm) geteilt ist. Sowohl zu dem digitus von 17,773 mm als auch zu dem digitus von 19,041 mm gibt es Ellen zu 28 und 30 digiti und Fuß-Einheiten zu 16 und 18 digiti.
XIII Aus der Teilung der 533,18 mm langen Elle in nur 24digiti erwuchs ein 16-digiti-Fuß von 533,18 mm : 24 x 16 = 355,45 mm. Es ist der Große Ptolemäische Fuß, Code E2.
XIV Auch aus dem Gudeafuß real entstanden andere Maßeinheiten. Weil er so kurz ist, (das war schon erwähnt) bildete man den philetärischen Fuß zu 20 digiti:
264,6 : 16 x 20 = 330,75 mm. Diese Fußlänge in 12 Unzen geteilt und dann auf nur 10 Unzen gestutzt, ergibt 330,75 : 12 x 10 = 275,63 mm/Fuß. Es ist der oskisch-umbrische Fuß, Code E3.
XV Das Maß von Abydos, Code J2, leitet sich von der Elle des Gudea dadurch ab, dass diese nicht in 30 Teile, wie üblich, sondern in 28 Teile (digiti), wie in Ägypten normal, geteilt wurde; dadurch wächst der digitus: 30 x 16, 587 mm = 497,61 mm (D2) 30 x 16,538 mm = 496,14 mm (D1)
497,61 mm : 28 = 17,772 mm496,14 mm : 28 = 17,719 mm
Das Maß von Abydos ist ein Doppelfuß-Maß, daher 2 x 18 digiti (2 pygme) = 36 digiti lang:
36 x 17,772 mm = 639,78 mm; 36 x 17,719 mm = 637,88 mm
xm = 638,83 mm.
638,83 mm : 2 = 319,42 mm
XVI Zwar war der 16-digiti-Fuß des Gudea 264,6 mm lang, doch hat man ihn anderenorts als einen 18-digiti-Fuß aufgefasst, wodurch der digitus noch kürzer wurde. Das hinwiederum wurde dadurch korrigiert, dass man zwar zunächst die Pygon, den 20-digiti-Fuß, bildete, dann diesen aber wie sonst üblich in 16 Teile teilte: 264,6 : 18 x 20 = 294,0 mm. Es ist der Punische Fuß, so benannt, weil die Insulae in Karthago nach ihm vermessen sind, Code
F1.
XVII Wie die Große Ptolemäische Elle zu 533,18 mm, Code E1, sich aus dem Gudeafuß entwickelt hat, ist unter XI dargestellt. Diese Ellenlänge wurde als 30-digiti-Elle verstanden, und dazu gab es auch die entsprechende pygme: 533,18 : 30 x 18 = 319,91 mm. Da solche Längen immer wieder falsch interpretiert wurden, im gegebenen Falle als 16-digiti-Fuß, konnte es im Bereich der Ellenlänge eine Umdeutung geben: 319,91 : 16 x 27 : 28 x 16 = 308,48 mm. Die Teilung durch 16 und anschließende Multiplikation mit 16 kann man sich selbstverständlich schenken, d.h. h. man kann 319,91 mit 27/28 multiplizieren, ohne über den digitus zu gehen, und erhält so den Kleinen Ptolemäischen Fuß, Code I 3.
Trotz seiner etwas verschlungenen Bildungsweise war er sehr viel gebraucht und gilt einigen als der griechische Fuß, was freilich nicht zutrifft.
XVIII Sehr direkt entsteht aus dem Gudea-Fuß real der bis zur Einführung des Meters in China gebräuchliche Fuß 'Tschi' : 264,6 : 10 x 12 = 317,50 mm, Code T. Es sieht aus, als wäre hier die sonst übliche Behandlungsweise 'westlicher' Maße rückwärts abgelaufen, denn diese, in 12 Unzen geteilt, wurden normalerweise auf 10 Unzen gestutzt. Allerdings wurden ab dem 9. Jh. 'westliche' Maßeinheiten ungekürzt übernommen (dafür gibt es eine Reihe Belege), und möglicherweise hat man den Gudea-Fuß für eine solcherart gekürzte Maßeinheit gehalten, weil er ja an sich recht kurz ist.
XIX Ähnlich umständlich wie der Kleine Ptolemäische Fuß hat sich auch der Vindonissa-Fuß aus dem Gudea-Fuß real entwickelt, wenngleich er später in anderen Gebieten ebenso beliebt war, besonders in der Schweiz von Römerzeiten an. Er kann sogar auf verschiedene Weise hergeleitet werden, was in der Literatur ausgebreitet ist. In der nachstehenden Formel stecken drei Umwandlungsschritte: a) : 28 x 30 betrifft die Ellenlänge; b) : 5 x 6 (= 10 x 12) betrifft eine Umformung des Fußes im Unzenbereich; c) :7 X 6 betrifft das Verhältnis 28 : 24, das heißt ein Wechsel von Königselle zu Handelselle. Die Formel:
265,4 : 28 x 30 : 5 x 6 : 7 x 6 = 292,48 mm, Code F3.
XX In Mesopotamien hatte man die Elle von 518,35 mm, Code A1, beibehalten, in Ägypten aber die Königselle zu 523,61 mm eingeführt. Für den Handel zwischen diesen Gebieten war das ständige Umrechnen zu lästig und deshalb bildete man einen Mittelwert aus diesen beiden Größen: (518,35 + 523,61) : 2 = 520,98 mm. Es ist die Kompromiss-Elle, Code F2, deren Fuß 297,70 mm lang ist. Da die Nippur-Elle nur rund 1 % von der Königselle abweicht, weicht die Kompromisselle nur 0,5 % von jeder der beiden ab. Für den Handel ist das zu vernachlässigen, nicht jedoch für theoretische Schlussfolgerungen, da sich aus der Kompromisselle andere Einheiten ableiten, die ihrerseits mit +/- 0,2 % Genauigkeit festliegen.
XXI Zum 16-digiti-Fuß des pes Romanus von 296,2 mm gibt es natürlich auch den 18-digiti-Fuß, die pygme. Es ist im griechischen Bereich der Kretisch-Äginetische Fuß, Code G, 333,2 mm lang, weil 296,2 mm : 16 x 18 = 333,2 mm. (vgl. III)
XXII Falls man den pes Drusianus statt durch 18, wie es an sich ‚richtig' wäre, nur durch 16 teilt, weil man ihn für einen ‚normalen' Fuß hält, erhält man einen ‚digitus' von 20,825 mm. Die zugehörige 30-digiti-Elle ist dann 20,825 mm x 30 = 624,75 mm lang. Ab dem vierten nachchristlichen Jahrhundert ist zu beobachten, dass die Elle in zwei Fuß unterteilt wurde. Im gegebenen Falle ergibt sich so 624,75 mm : 2 = 312,375 mm, gerundet 312,4 mm. Dieser Fuß erhielt, da er erst spät im byzantinischen Reich verwendet wurde, die Bezeichnung ‚spätbyzantinischer Fuß' und wegen seiner Genese den Code G2.
XXIII Die Kompromisselle, Code F2, war als 28-digiti-Elle entstanden. Dennoch wurde sie später als 24-digiti-Elle aufgefasst, wodurch der digitus stark anwuchs: 520,98 : 24 = 21,708 mm. Aus diesem digitus wurde dann eine neue Fußlänge zu 16 digiti gebildet: 21,708 x 16 = 347,32 mm. Es ist der samisch-ionische Fuß, Code I 2.
XXIV Wie der Vindonissa-Fuß, Code F3, lässt sich auch die 'Neue Elle' auf verschiedenen Wegen herleiten. Wenn man die pygon des Kompromissfußes, Code F2, bildet : 520,98 : 7 x 5 = 372,15 mm und diese, wie bei der Bildung der Königselle aus der Nippur-Elle als Seite eines Quadrats nimmt, dann wird die Diagonale 526,27 mm lang. Oder 520,98 x 1,0102 = 526,29 mm. Das ist die normal in 28 digiti geteilte 'Neue Elle', Code J1. Ihr Fuß ist 526,29 : 28 x 16 = 300,73 mm.
Die 24-digiti-Elle der Salamiselle, Code A4, ist 483,8 mm lang, obwohl sie zunächst eine 28-digiti-Elle war. Ihr digitus ist daher 483,8 : 24 = 20,158. Daraus wird nun wieder eine 28-digiti-Elle gebildet, und so ergibt das 20,158 x 28 = 564,43 mm. Diese Länge wiederum als 30 digiti betrachtet - wodurch der digitus kleiner wird: 18,814 mm - und erneut mit 28 multipliziert, ergibt dann 526,80 mm pro Elle. Das weicht von der obigen Herleitung um 0,097 % ab. Was nun genau in der fast fünftausendjährigen Geschichte abgelaufen ist, bis dieser Fuß dann bei den Griechen fassbar wird, lässt sich nicht genau sagen.
XXV Teilt man die Ellenlänge von 526,80 mm, Code J1, (vergl. XXII) in 30 digiti auf, dann wird der digitus 17,56 mm lang. Aus diesem digitus wurde zunächst ein 18-digiti-Fuß gebildet, eine pygme, die dann 17,56 x 18 = 316,08 mm lang ist. Als diese Fußlänge in den Einflussbereich der Griechen kam, haben sie sie wie üblich als in nur 16 digiti geteilt aufgefasst, weswegen es sowohl eine pygme als auch einen 'normalen' 16-digiti-Fuß von 316,08 mm Länge gibt. Das ist sehr verwirrend, aber ein typisches Schicksal von Maßeinheiten, die sehr lange verwendet wurden. Es ist der gemeingriechische Fuß, Code ebenfalls noch J1. Die zugehörige Elle ist 553,14 mm lang.
XXVI Die Große Ägyptische Königselle, Code B2, ist eine 28-digiti-Elle von 528,9 mm Länge, weswegen ihr digitus 528,90 : 28 = 18,889 mm lang ist. Um eine 30-digiti-Elle zu erhalten, muss man mit 30 multiplizieren: 18,889 x 30 = 566,68 mm. Der zugehörige Fuß ist, wenn man die Elle nun wieder als 28-digiti-Elle betrachtet 566,68 : 28 x 16 = 323,8 mm. So lang war der Pied de Roi ursprünglich. Im Verlaufe der Zeit wurde er etwas länger und stieg auf 324,8 mm. Dies geschah in politisch unruhigen Zeiten nach dem Zusammenbruch des Römischen Weltreiches. Die Abweichung nach oben beträgt 0,30 %. Es ist die zweitgrößte Abweichung in der Geschichte der Metrologie. Danach aber blieb der Pied de Roi, Code I 1, bemerkenswert stabil.
XXVII Ursprünglich war die Ägyptische Königselle eine 28-digiti-Elle. Außerhalb Ägyptens wurde sie aber als 30-digiti-Elle behandelt; ihr digitus schrumpfte auf 523,61 : 30 = 17.453 mm. Die dazu gehörende pygme, also der 18-digiti-Fuß, ist 17,453 x 18 = 314,15 mm lang. Es ist der 'Äginetische Fuß’, Code H2.
XXVIII Man kann aus der Ägyptischen Königselle eine 30-digiti-Elle auch so machen, dass man 2 digiti zufügt: 523,61 : 28 x 30 = 561,00 mm. Der Fuß ist dann 561,00 : 28 x 16 = 320,57 mm lang. Es ist der Byzantinische Fuß, Code J3.
XXIX Der Pythische Fuß ist eine etwas exotische Bildung. Es beruhte ursprünglich auf Getreidekörnern. Die Nippur-Elle, Code A1, wird zunächst mit 6 multipliziert, als ob sie ein Fuß sei und so ein Klafter gebildet werden müsste. Sodann wird durch 100 geteilt, um den 'digitus' zu erhalten. 518,35 x 6 : 100 = 31,101 mm. Das ergibt, mit 16 multipliziert, 497,62 mm. Weil diese Länge im Bereich der Doppelfußmaße liegt, wurde noch durch 2 dividiert, um in den Bereich der Fußlängen zu kommen: 248,81 mm. Code P Dem Ganzen liegt eine Dreier-Teilung zugrunde: 3 Gerstenkörner ergeben einen Daumen, 3 Daumen ergeben eine palma, 3 palmae ergeben den Fuß, so dass dieser 27 Gerstenkörner hat.
XXX Das Indus-Maß ist sehr eng mit der Nipur-Elle, Code A1, verknüpft. Die Unterschiede treten dadurch auf, dass das Indus-Maß dekadisch geteilt ist. Die palma der Nippur-Elle ist 518,35 : 30 x 4 = 69,113 mm lang; die Elle selbst 7,5 palmae. Diese palma ist das Verbindungsstück zum Indus-Maß, denn dieses teilt einerseits diese palma in 10 'digiti', wenn man so will, andererseits sind 5 palmae 5 x 69,113 mm = 345,57 mm, und das entspricht der pygon der Nippur-Elle oder mit anderen Worten 2/3 der Nippur-Elle. Fasst man 345,57, wie das anderenorts geschehen ist, als 16-digiti-Fuß auf, dann ist der digitus 345,57 : 16 = 21,598 mm lang, und die daraus gebildete Handelselle zu 24 digiti ist 21,598 x 24 = 518,35 mm lang, also wieder gleich der Nippur-Elle. 2 x 345,57 = 691,14 mm ist die nächsthöhere Obereinheit des Indusmaßes im Längenbereich der Doppelfußmaße, Code K.
XXXI Aus der Spätzeit Ägyptens gibt es zwei Maßstäbe, die offenbar keine weite Verbreitung gefunden haben. Soweit bekannt, sind keine Bauwerke nach diesen Maßeinheiten ausgeführt worden. Sie haben auch keine uns bekannten Namen, weswegen sie mit Code N1 und Code N2 bezeichnet werden. So exotisch diese Maßstäbe sind, so exotisch ist auch ihre Ableitung: Zunächst muss der Nippur-Fuß genommen werden: 518,35 : 30 x 16 = 276,45. Diese Länge ist dann, ähnlich wie seinerzeit beim Rohr der Nippur-Elle, zunächst mit 6 multipliziert worden, was ja das Klafter ergibt, und dann durch 100 geteilt worden, wodurch ein digitus entsteht. Durch Multiplikation mit 32 entstand eine Doppelfußlänge, und durch Multiplikation mit 1,01015 wird wieder die Diagonale im Quadrat erreicht. Nur dies letztere ist typisch für Ägypten. Die Formel für N1 lautet dann: 518,35 : 30 x 16 x 6 : 100 x 32 x 1,01015 = 536,18 mm. Um N2 zu erhalten, muss noch einmal mit 1,01015 multipliziert werden: 536,18 x 1,01015 = 541,62 mm.
Eine Zusammenfassung gibt die folgende Abbildung, zum Vergrößern klicken Sie bitte auf das Bild
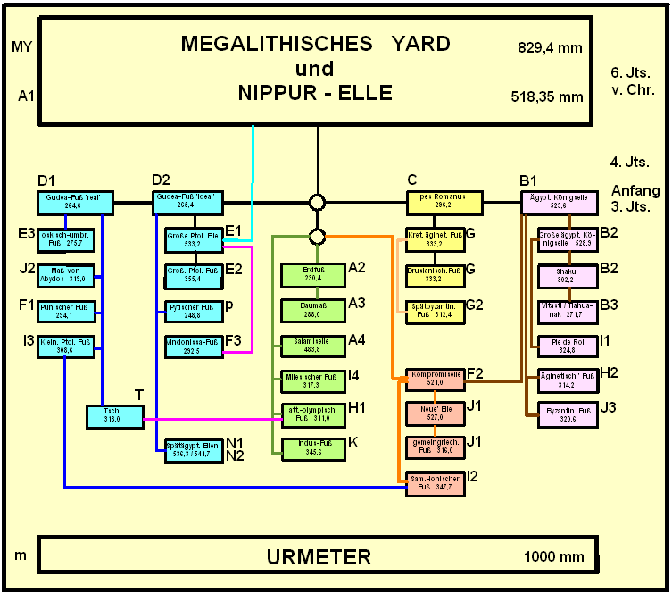
Die folgende Tabelle zeigt die mathematische Berechnung der Maßeinhaiten aus dem Bestwert der Nippur_elle resp. auseinander:

nach oben
vorige Seite zum Inhaltsverzeichnis nächste Seite
|


